|
2 | 2 |
|
3 | 3 |  [](https://codecov.io/github/lucasimi/tda-mapper-python) |
4 | 4 |
|
5 | | -In recent years, an ever growing interest in **Topological Data Analysis** (TDA) emerged in the field of data science. The core principle of TDA is to gain insights from data by using topological methods, as they show good resilience to noise, and they are often more stable than many traditional techniques. This Python package provides an implementation of the **Mapper Algorithm**, one of the most common tools from TDA. |
| 5 | +In recent years, an ever growing interest in **Topological Data Analysis** (TDA) emerged in the field of data science. The core idea of TDA is to gain insights from data by using topological methods that are proved to be reliable with respect to noise, and that behave nicely with respect to dimension. This Python package provides an implementation of the **Mapper Algorithm**, a well-known tool from TDA. |
6 | 6 |
|
7 | | -The mapper algorithm takes any dataset $X$ (usually high dimensional), and returns a graph $G$, called **Mapper Graph**. Surprisingly enough, despite living in a 2-dimensional space, the mapper graph $G$ represents a reliable summary for the shape of $X$ (they share the same number of connected components). This feature makes the mapper algorithm a very appealing choice over more traditional approaches, for example those based on projections, because they often give you no way to control shape distortions. Moreover, preventing artifacts is especially important for data visualization: the mapper graph is often a capable tool, which can help you identify hidden patterns in high-dimensional data. |
| 7 | +The Mapper Algorithm takes any dataset $X$ and returns a *shape-summary* in the form a graph $G$, called **Mapper Graph**. It's possible to prove, under reasonable conditions, that $X$ and $G$ share the same number of connected components. |
8 | 8 |
|
9 | 9 | ## Basics |
10 | 10 |
|
11 | | -Here we'll give just a brief description of the core ideas around the mapper, but the interested reader is advised to take a look at the original [paper](https://research.math.osu.edu/tgda/mapperPBG.pdf). The Mapper Algorithm follows these steps: |
| 11 | +Let $f$ be any chosen *lens*, i.e. a continuous map $f \colon X \to Y$, being $Y$ any parameter space (*typically* low dimensional). In order to build the Mapper Graph follow these steps: |
12 | 12 |
|
13 | | -1. Take any *lens* you want. A lens is just a continuous map $f \colon X \to Y$, where $Y$ is any parameter space, usually having dimension lower than $X$. You can think of $f$ as a set of KPIs, or features of particular interest for the domain of study. Some common choices for $f$ are *statistics* (of any order), *projections*, *entropy*, *density*, *eccentricity*, and so forth. |
| 13 | +1. Build an *open cover* for $f(X)$, i.e. a collection of *open sets* whose union makes the whole image $f(X)$. |
14 | 14 |
|
15 | | -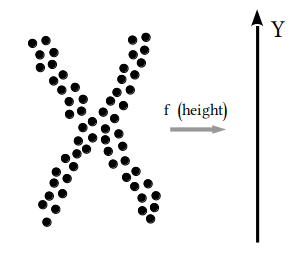 |
| 15 | +2. Run clustering on the preimage of each open set. All these local clusters together make a *refined open cover* for $X$. |
16 | 16 |
|
17 | | -2. Build an *open cover* for $f(X)$. An open cover is a collection of open sets (like open balls, or open intervals) whose union makes the whole image $f(X)$, and can possibly intersect. |
| 17 | +3. Build the mapper graph $G$ by taking a node for each local cluster, and by drawing an edge between two nodes whenever their corresponding local clusters intersect. |
18 | 18 |
|
19 | | - |
| 19 | +To get an idea, in the following picture we have $X$ as an X-shaped point cloud in $\mathbb{R}^2$, with $f$ being the *height function*, i.e. the projection on the $y$-axis. In the leftmost part we cover the projection of $X$ with three open sets. Every open set is represented with a different color. Then we take the preimage of these sets, cluster then, and finally build the graph according to intersections. |
20 | 20 |
|
21 | | -3. For each element $U$ of the open cover of $f(X)$, let $f^{-1}(U)$ be the preimage of $U$ under $f$. Then the collection of all the $f^{-1}(U)$'s makes an open cover of $X$. At this point, split every preimage $f^{-1}(U)$ into clusters, by running any chosen *clustering* algorithm, and keep track of all the local clusters obtained. All these local clusters together make a *refined open cover* for $X$. |
| 21 | + |
22 | 22 |
|
23 | | - |
24 | | - |
25 | | -4. Build the mapper graph $G$ by taking a node for each local cluster, and by drawing an edge between two nodes whenever their corresponding local clusters intersect. |
26 | | - |
27 | | -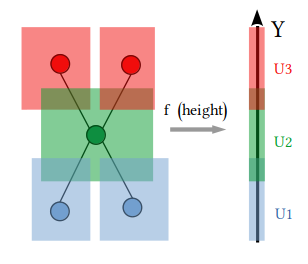 |
28 | | - |
29 | | -N.B.: The choice of the lens $f$ has a deep practical impact on the mapper graph. Theoretically, if clusters were able to perfectly identify connected components (and if they were "reasonably well behaved"), chosing any $f$ would give the same mapper graph (see the [Nerve Theorem](https://en.wikipedia.org/wiki/Nerve_complex#Nerve_theorems) for a more precise statement). In this case, there would be no need for a tool like the mapper, since clustering algorithms would provide a complete tool to understand the shape of data. Unfortunately, clustering algorithms are not that good. Think for example about the case of $f$ being a constant function: in this case computing the mapper graph would be equivalent to performing clustering on the whole dataset. For this reason a good choice for $f$ would be any continuous map which is somewhat *sensible* to data: the more sublevel sets are apart, the higher the chance of a good local clustering. |
| 23 | +The choice of the lens is the most relevant on the shape of the Mapper Graph. Some common choices are *statistics*, *projections*, *entropy*, *density*, *eccentricity*, and so forth. However, in order to pick a good lens, specific domain knowledge for the data at hand can give a hint. For an in-depth description of Mapper please read [the original paper](https://research.math.osu.edu/tgda/mapperPBG.pdf). |
30 | 24 |
|
31 | 25 | ## Installation |
32 | 26 |
|
33 | | -First, clone this repo, `cd` into the local repo, and install via `pip` from your local repo |
| 27 | +Clone this repo, and install via `pip` from your local directory |
34 | 28 | ``` |
35 | 29 | python -m pip install . |
36 | 30 | ``` |
| 31 | +Alternatively, you can use `pip` to install directly from GitHub |
| 32 | +``` |
| 33 | +pip install git+https://github.com/lucasimi/tda-mapper-python.git |
| 34 | +``` |
| 35 | +If you want to install the version from a specific branch, for example `develop`, you can run |
| 36 | +``` |
| 37 | +pip install git+https://github.com/lucasimi/tda-mapper-python.git@develop |
| 38 | +``` |
37 | 39 |
|
38 | | -## How to use this package - A First Example |
| 40 | +## A worked out example |
39 | 41 |
|
40 | | -In the following example, we use the mapper to perform some analysis on the famous Iris dataset. This dataset consists of 150 records, having 4 numerical features and a label which represents a class. As lens, we chose the PCA on two components. |
| 42 | +In order to show how to use this package, we perform some analysis on the the well known dataset of hand written digits (more info [here](https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_digits.html)), consisting of less than 2000 8x8 pictures represented as arrays of 64 elements. |
41 | 43 |
|
42 | 44 | ```python |
43 | | -from sklearn.datasets import load_iris |
| 45 | +import numpy as np |
| 46 | + |
| 47 | +from sklearn.datasets import load_digits |
44 | 48 | from sklearn.cluster import AgglomerativeClustering |
45 | 49 | from sklearn.decomposition import PCA |
46 | 50 |
|
47 | | -import matplotlib |
48 | | - |
49 | 51 | from tdamapper.core import * |
50 | 52 | from tdamapper.cover import * |
51 | 53 | from tdamapper.clustering import * |
52 | 54 | from tdamapper.plot import * |
53 | 55 |
|
54 | | -iris_data = load_iris() |
55 | | -X, y = iris_data.data, iris_data.target |
56 | | -lens = PCA(2).fit_transform(X) |
| 56 | +import matplotlib |
57 | 57 |
|
58 | | -cover = CubicCover(n_intervals=7, overlap_frac=0.25) |
59 | | -clustering = AgglomerativeClustering(n_clusters=2, linkage='single') |
| 58 | +digits = load_digits() |
| 59 | +X, y = [np.array(x) for x in digits.data], digits.target |
| 60 | +lens = PCA(2).fit_transform(X) |
60 | 61 |
|
61 | | -mapper_algo = MapperAlgorithm(cover, clustering) |
| 62 | +mapper_algo = MapperAlgorithm( |
| 63 | + cover=GridCover(n_intervals=10, overlap_frac=0.65), |
| 64 | + clustering=AgglomerativeClustering(10), |
| 65 | + verbose=True, |
| 66 | + n_jobs=8) |
62 | 67 | mapper_graph = mapper_algo.fit_transform(X, lens) |
63 | | -mapper_plot = MapperPlot(X, mapper_graph) |
64 | | -colored = mapper_plot.with_colors(colors=list(y), agg=np.nanmedian) |
65 | 68 |
|
66 | | -fig, ax = plt.subplots(1, 1, figsize=(7, 7)) |
67 | | -colored.plot_static(title='class', ax=ax) |
| 69 | +mapper_plot = MapperPlot(X, mapper_graph, |
| 70 | + colors=y, |
| 71 | + cmap='jet', |
| 72 | + agg=np.nanmean, |
| 73 | + dim=2, |
| 74 | + iterations=400) |
| 75 | +fig_mean = mapper_plot.plot(title='digit (mean)', width=600, height=600) |
| 76 | +fig_mean.show(config={'scrollZoom': True}) |
68 | 77 | ``` |
69 | 78 |
|
70 | | -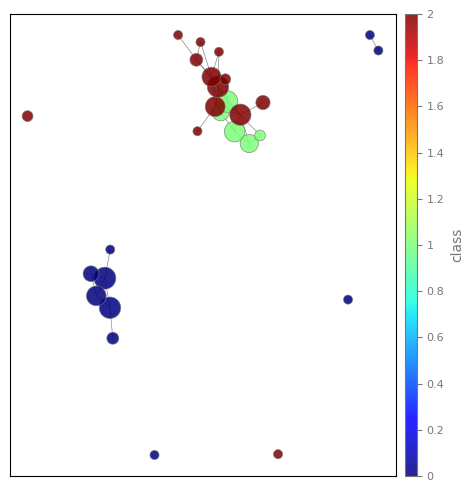 |
71 | | - |
72 | | -As you can see from the plot, we can identify two major connected components, one which corresponds precisely to a single class, and the other which is shared by the other two classes. |
| 79 | + |
73 | 80 |
|
74 | | -## A Second Example |
75 | | - |
76 | | -In this second example we try to take a look at the shape of the digits dataset. This dataset consists of less than 2000 pictures of handwritten digits, represented as dim-64 arrays (8x8 pictures) |
| 81 | +It's also possible to obtain a new plot colored according to different values, while keeping the same computed geometry. For example, if we want to visualize how much dispersion we have on each cluster, we could plot colors according to the standard deviation |
77 | 82 |
|
78 | 83 | ```python |
79 | | -from sklearn.datasets import load_digits |
80 | | -from sklearn.cluster import KMeans |
81 | | -from sklearn.decomposition import PCA |
82 | | - |
83 | | -from tdamapper.core import * |
84 | | -from tdamapper.cover import * |
85 | | -from tdamapper.clustering import * |
86 | | -from tdamapper.plot import * |
87 | | - |
88 | | -import matplotlib |
89 | | - |
90 | | -digits = load_digits() |
91 | | -X, y = [np.array(x) for x in digits.data], digits.target |
92 | | -lens = PCA(2).fit_transform(X) |
| 84 | +fig_std = mapper_plot.with_colors( |
| 85 | + colors=y, |
| 86 | + cmap='viridis', |
| 87 | + agg=np.nanstd, |
| 88 | +).plot(title='digit (std)', width=600, height=600) |
| 89 | +fig_std.show(config={'scrollZoom': True}) |
| 90 | +``` |
93 | 91 |
|
94 | | -cover = CubicCover(n_intervals=15, overlap_frac=0.25) |
95 | | -clustering = KMeans(10, n_init='auto') |
| 92 | + |
96 | 93 |
|
97 | | -mapper_algo = MapperAlgorithm(cover, clustering) |
98 | | -mapper_graph = mapper_algo.fit_transform(X, lens) |
99 | | -mapper_plot = MapperPlot(X, mapper_graph, iterations=100) |
| 94 | +The mapper graph of the digits dataset shows a few interesting patterns. For example, we can make the following observations: |
100 | 95 |
|
101 | | -fig = mapper_plot.with_colors(colors=y, cmap='jet', agg=np.nanmedian).plot_interactive_2d(title='digit', width=512, height=512) |
102 | | -fig.show(config={'scrollZoom': True}) |
103 | | -``` |
104 | | - |
105 | | - |
| 96 | +* Clusters that share the same color are all connected together, and located in the same area of the graph. This behavior is present in those digits which are easy to tell apart from the others, for example digits 0 and 4. |
106 | 97 |
|
107 | | -As you can see the mapper graph shows interesting patterns. Note that the shape of the graph is obtained by looking only at the 8x8 pictures, discarding any information about the actual label (the digit). You can see that those local clusters which share the same labels are located in the same area of the graph. This tells you (as you would expect) that the labelling is *compatible with the shape of data*. |
| 98 | +* Some clusters are not well separated and tend to overlap one on the other. This mixed behavior is present in those digits which can be easily confused one with the other, for example digits 5 and 6. |
108 | 99 |
|
109 | | - |
| 100 | +* Clusters located across the "boundary" of two different digits show a transition either due to a change in distribution or due to distorsions in the hand written text, for example digits 8 and 2. |
110 | 101 |
|
111 | | -Moreover, by zooming in, you can see that some clusters are located next to others. For example in the picture you can see the details of digits '4' (cyan) and '7' (red) being located one next to the other. |
112 | 102 |
|
113 | 103 | ### Development - Supported Features |
114 | 104 |
|
115 | 105 | - [x] Topology |
116 | | - - [x] Any custom lens |
117 | | - - [x] Any custom metric |
| 106 | + - [x] custom lenses |
| 107 | + - [x] custom metrics |
| 108 | + |
118 | 109 | - [x] Cover algorithms: |
119 | | - - [x] Cubic Cover |
120 | | - - [x] Ball Cover |
121 | | - - [x] Knn Cover |
| 110 | + - [x] `GridCover` |
| 111 | + - [x] `BallCover` |
| 112 | + - [x] `KnnCover` |
| 113 | + |
122 | 114 | - [x] Clustering algoritms |
123 | | - - [x] Any sklearn clustering algorithm |
124 | | - - [x] Skip clustering |
125 | | - - [x] Clustering induced by cover |
| 115 | + - [x] `sklearn.cluster`-compatible algorithms |
| 116 | + - [x] `TrivialClustering` to skip clustering |
| 117 | + - [x] `CoverClustering` for clustering induced by cover |
| 118 | + |
| 119 | +- [x] Plot |
| 120 | + - [x] 2d interactive plot |
| 121 | + - [x] 3d interactive plot |
| 122 | + - [ ] HTML embeddable plot |
0 commit comments