Binary Logical Graph Operators

This section provides an overview of binary graph operators, which consume two graphs as input.

Binary Logical Graph Operators
Combination
Overlap
Exclusion
Equality
VertexFusion

Combination

Given two graphs, the combine operator creates a LogicalGraph that includes the edges and vertices of both graphs. It is implemented by the combine() function of the LogicalGraph. The combine function takes a LogicalGraph as its input and outputs a new LogicalGraph that includes the elements of both graphs.

Combine example

Consider the social graph from our quickstart section.
We use the combine function to retrieve all Person older than 30 of both graphs.

// Combine both graphs
LogicalGraph combination = n1.combine(n2)
    // Retrieve the persons that are older than 30
    .subgraph(
            v -> v.getLabel().equals("Person") && v.getPropertyValue("age").getInt() >= 30,
            e -> false
    );

The resulting graph looks as follows:

Overlap

Given two graphs, the overlap operator extracts their common vertices and edges resulting in a new LogicalGraph. It is implemented by the overlap() function of the LogicalGraph. The overlap function takes a LogicalGraph as its input and outputs a new LogicalGraph consisting of the common elements in both graphs.

Overlap example

Consider the social graph from our quickstart section.
We use the overlap function to retrieve the common elements in both graphs.

LogicalGraph overlap = n2.overlap(n1);

The resulting graph looks as follows:

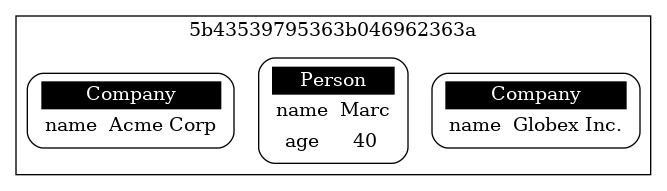
The overlap graph contains all the common elements of both graphs. There are no common vertices in g1 and g2, hence there are no vertices in the overlap graph.

Exclusion

Given two graphs a and b, the exclusion operator creates a LogicalGraph that includes the edges and vertices of graph a that do not occur in graph b. It is implemented by the exclude() function of the LogicalGraph. The exclude function takes a LogicalGraph as its input and outputs a new LogicalGraph consisting of the elemtents of graph a without the elements of graph b.

Exclusion example

Consider the social graph from our quickstart section.
We use the exclude function to retrieve all elements from graph n1 that do not occur in n2.

LogicalGraph exlusion = n1.exclude(n2);

The resulting graph looks as follows:

Equality

Given two graphs, the equality operator determines whether they are equal. The operator is implemented by the LogicalGraph. The equal operator takes another Logical Graph as its input and outputs a DataSet<Boolean> that contains a single boolean value.

Method	Description
equalsByData	Compares the vertices, edges and the label, properties of the `LogicalGraphs` for equality.
equalsByElementData	Compares the vertices and edges of the `LogicalGraphs` for equality.
equalsByElementIds	Compares the vertices and edges of the `LogicalGraphs` for equality by using their internal ID. Therefore, 2 graphs may have vertices and edges with the same properties without being equal.