|
| 1 | +# Neural Stochastic Differential Equations With Method of Moments |
| 2 | + |
| 3 | +With neural stochastic differential equations, there is once again a helper form |
| 4 | +`neural_dmsde` which can be used for the multiplicative noise case (consult the |
| 5 | +layers API documentation, or [this full example using the layer |
| 6 | +function](https://github.com/MikeInnes/zygote-paper/blob/master/neural_sde/neural_sde.jl)). |
| 7 | + |
| 8 | +However, since there are far too many possible combinations for the API to |
| 9 | +support, in many cases you will want to performantly define neural differential |
| 10 | +equations for non-ODE systems from scratch. For these systems, it is generally |
| 11 | +best to use `TrackerAdjoint` with non-mutating (out-of-place) forms. For |
| 12 | +example, the following defines a neural SDE with neural networks for both the |
| 13 | +drift and diffusion terms: |
| 14 | + |
| 15 | +```julia |
| 16 | +dudt(u, p, t) = model(u) |
| 17 | +g(u, p, t) = model2(u) |
| 18 | +prob = SDEProblem(dudt, g, x, tspan, nothing) |
| 19 | +``` |
| 20 | + |
| 21 | +where `model` and `model2` are different neural networks. The same can apply to |
| 22 | +a neural delay differential equation. Its out-of-place formulation is |
| 23 | +`f(u,h,p,t)`. Thus for example, if we want to define a neural delay differential |
| 24 | +equation which uses the history value at `p.tau` in the past, we can define: |
| 25 | + |
| 26 | +```julia |
| 27 | +dudt!(u, h, p, t) = model([u; h(t - p.tau)]) |
| 28 | +prob = DDEProblem(dudt_, u0, h, tspan, nothing) |
| 29 | +``` |
| 30 | + |
| 31 | + |
| 32 | +First let's build training data from the same example as the neural ODE: |
| 33 | + |
| 34 | +```@example nsde |
| 35 | +using Plots, Statistics |
| 36 | +using Flux, Optimization, OptimizationFlux, DiffEqFlux, StochasticDiffEq, SciMLBase.EnsembleAnalysis |
| 37 | +
|
| 38 | +u0 = Float32[2.; 0.] |
| 39 | +datasize = 30 |
| 40 | +tspan = (0.0f0, 1.0f0) |
| 41 | +tsteps = range(tspan[1], tspan[2], length = datasize) |
| 42 | +``` |
| 43 | + |
| 44 | +```@example nsde |
| 45 | +function trueSDEfunc(du, u, p, t) |
| 46 | + true_A = [-0.1 2.0; -2.0 -0.1] |
| 47 | + du .= ((u.^3)'true_A)' |
| 48 | +end |
| 49 | +
|
| 50 | +mp = Float32[0.2, 0.2] |
| 51 | +function true_noise_func(du, u, p, t) |
| 52 | + du .= mp.*u |
| 53 | +end |
| 54 | +
|
| 55 | +prob_truesde = SDEProblem(trueSDEfunc, true_noise_func, u0, tspan) |
| 56 | +``` |
| 57 | + |
| 58 | +For our dataset we will use DifferentialEquations.jl's [parallel ensemble |
| 59 | +interface](http://docs.juliadiffeq.org/dev/features/ensemble.html) to generate |
| 60 | +data from the average of 10,000 runs of the SDE: |
| 61 | + |
| 62 | +```@example nsde |
| 63 | +# Take a typical sample from the mean |
| 64 | +ensemble_prob = EnsembleProblem(prob_truesde) |
| 65 | +ensemble_sol = solve(ensemble_prob, SOSRI(), trajectories = 10000) |
| 66 | +ensemble_sum = EnsembleSummary(ensemble_sol) |
| 67 | +
|
| 68 | +sde_data, sde_data_vars = Array.(timeseries_point_meanvar(ensemble_sol, tsteps)) |
| 69 | +``` |
| 70 | + |
| 71 | +Now we build a neural SDE. For simplicity we will use the `NeuralDSDE` |
| 72 | +neural SDE with diagonal noise layer function: |
| 73 | + |
| 74 | +```@example nsde |
| 75 | +drift_dudt = Flux.Chain(x -> x.^3, |
| 76 | + Flux.Dense(2, 50, tanh), |
| 77 | + Flux.Dense(50, 2)) |
| 78 | +p1, re1 = Flux.destructure(drift_dudt) |
| 79 | +
|
| 80 | +diffusion_dudt = Flux.Chain(Flux.Dense(2, 2)) |
| 81 | +p2, re2 = Flux.destructure(diffusion_dudt) |
| 82 | +
|
| 83 | +neuralsde = NeuralDSDE(drift_dudt, diffusion_dudt, tspan, SOSRI(), |
| 84 | + saveat = tsteps, reltol = 1e-1, abstol = 1e-1) |
| 85 | +``` |
| 86 | + |
| 87 | +Let's see what that looks like: |
| 88 | + |
| 89 | +```@example nsde |
| 90 | +# Get the prediction using the correct initial condition |
| 91 | +prediction0 = neuralsde(u0) |
| 92 | +
|
| 93 | +drift_(u, p, t) = re1(p[1:neuralsde.len])(u) |
| 94 | +diffusion_(u, p, t) = re2(p[neuralsde.len+1:end])(u) |
| 95 | +
|
| 96 | +prob_neuralsde = SDEProblem(drift_, diffusion_, u0,(0.0f0, 1.2f0), neuralsde.p) |
| 97 | +
|
| 98 | +ensemble_nprob = EnsembleProblem(prob_neuralsde) |
| 99 | +ensemble_nsol = solve(ensemble_nprob, SOSRI(), trajectories = 100, |
| 100 | + saveat = tsteps) |
| 101 | +ensemble_nsum = EnsembleSummary(ensemble_nsol) |
| 102 | +
|
| 103 | +plt1 = plot(ensemble_nsum, title = "Neural SDE: Before Training") |
| 104 | +scatter!(plt1, tsteps, sde_data', lw = 3) |
| 105 | +
|
| 106 | +scatter(tsteps, sde_data[1,:], label = "data") |
| 107 | +scatter!(tsteps, prediction0[1,:], label = "prediction") |
| 108 | +``` |
| 109 | + |
| 110 | +Now just as with the neural ODE we define a loss function that calculates the |
| 111 | +mean and variance from `n` runs at each time point and uses the distance from |
| 112 | +the data values: |
| 113 | + |
| 114 | +```@example nsde |
| 115 | +function predict_neuralsde(p, u = u0) |
| 116 | + return Array(neuralsde(u, p)) |
| 117 | +end |
| 118 | +
|
| 119 | +function loss_neuralsde(p; n = 100) |
| 120 | + u = repeat(reshape(u0, :, 1), 1, n) |
| 121 | + samples = predict_neuralsde(p, u) |
| 122 | + means = mean(samples, dims = 2) |
| 123 | + vars = var(samples, dims = 2, mean = means)[:, 1, :] |
| 124 | + means = means[:, 1, :] |
| 125 | + loss = sum(abs2, sde_data - means) + sum(abs2, sde_data_vars - vars) |
| 126 | + return loss, means, vars |
| 127 | +end |
| 128 | +``` |
| 129 | + |
| 130 | +```@example nsde |
| 131 | +list_plots = [] |
| 132 | +iter = 0 |
| 133 | +
|
| 134 | +# Callback function to observe training |
| 135 | +callback = function (p, loss, means, vars; doplot = false) |
| 136 | + global list_plots, iter |
| 137 | +
|
| 138 | + if iter == 0 |
| 139 | + list_plots = [] |
| 140 | + end |
| 141 | + iter += 1 |
| 142 | +
|
| 143 | + # loss against current data |
| 144 | + display(loss) |
| 145 | +
|
| 146 | + # plot current prediction against data |
| 147 | + plt = Plots.scatter(tsteps, sde_data[1,:], yerror = sde_data_vars[1,:], |
| 148 | + ylim = (-4.0, 8.0), label = "data") |
| 149 | + Plots.scatter!(plt, tsteps, means[1,:], ribbon = vars[1,:], label = "prediction") |
| 150 | + push!(list_plots, plt) |
| 151 | +
|
| 152 | + if doplot |
| 153 | + display(plt) |
| 154 | + end |
| 155 | + return false |
| 156 | +end |
| 157 | +``` |
| 158 | + |
| 159 | +Now we train using this loss function. We can pre-train a little bit using a |
| 160 | +smaller `n` and then decrease it after it has had some time to adjust towards |
| 161 | +the right mean behavior: |
| 162 | + |
| 163 | +```@example nsde |
| 164 | +opt = ADAM(0.025) |
| 165 | +
|
| 166 | +# First round of training with n = 10 |
| 167 | +adtype = Optimization.AutoZygote() |
| 168 | +optf = Optimization.OptimizationFunction((x,p) -> loss_neuralsde(x, n=10), adtype) |
| 169 | +optprob = Optimization.OptimizationProblem(optf, neuralsde.p) |
| 170 | +result1 = Optimization.solve(optprob, opt, |
| 171 | + callback = callback, maxiters = 100) |
| 172 | +``` |
| 173 | + |
| 174 | +We resume the training with a larger `n`. (WARNING - this step is a couple of |
| 175 | +orders of magnitude longer than the previous one). |
| 176 | + |
| 177 | +```@example nsde |
| 178 | +optf2 = Optimization.OptimizationFunction((x,p) -> loss_neuralsde(x, n=100), adtype) |
| 179 | +optprob2 = Optimization.OptimizationProblem(optf2, result1.u) |
| 180 | +result2 = Optimization.solve(optprob2, opt, |
| 181 | + callback = callback, maxiters = 100) |
| 182 | +``` |
| 183 | + |
| 184 | +And now we plot the solution to an ensemble of the trained neural SDE: |
| 185 | + |
| 186 | +```@example nsde |
| 187 | +_, means, vars = loss_neuralsde(result2.u, n = 1000) |
| 188 | +
|
| 189 | +plt2 = Plots.scatter(tsteps, sde_data', yerror = sde_data_vars', |
| 190 | + label = "data", title = "Neural SDE: After Training", |
| 191 | + xlabel = "Time") |
| 192 | +plot!(plt2, tsteps, means', lw = 8, ribbon = vars', label = "prediction") |
| 193 | +
|
| 194 | +plt = plot(plt1, plt2, layout = (2, 1)) |
| 195 | +savefig(plt, "NN_sde_combined.png"); nothing # sde |
| 196 | +``` |
| 197 | + |
| 198 | +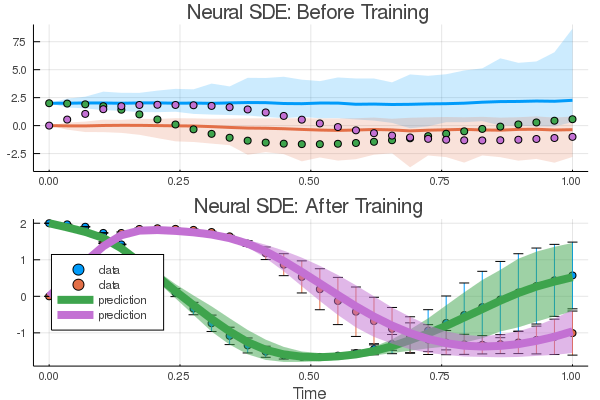 |
| 199 | + |
| 200 | +Try this with GPUs as well! |
0 commit comments