|
| 1 | +# Multiple Shooting |
| 2 | + |
| 3 | +In Multiple Shooting, the training data is split into overlapping intervals. |
| 4 | +The solver is then trained on individual intervals. If the end conditions of any |
| 5 | +interval coincide with the initial conditions of the next immediate interval, |
| 6 | +then the joined/combined solution is same as solving on the whole dataset |
| 7 | +(without splitting). |
| 8 | + |
| 9 | +To ensure that the overlapping part of two consecutive intervals coincide, |
| 10 | +we add a penalizing term, `continuity_term * absolute_value_of(prediction |
| 11 | +of last point of group i - prediction of first point of group i+1)`, to |
| 12 | +the loss. |
| 13 | + |
| 14 | +Note that the `continuity_term` should have a large positive value to add |
| 15 | +high penalties in case the solver predicts discontinuous values. |
| 16 | + |
| 17 | + |
| 18 | +The following is a working demo, using Multiple Shooting |
| 19 | + |
| 20 | +```julia |
| 21 | +using Lux, DiffEqFlux, Optimization, OptimizationPolyalgorithms, DifferentialEquations, Plots |
| 22 | +using DiffEqFlux: group_ranges |
| 23 | + |
| 24 | +using Random |
| 25 | +rng = Random.default_rng() |
| 26 | + |
| 27 | +# Define initial conditions and time steps |
| 28 | +datasize = 30 |
| 29 | +u0 = Float32[2.0, 0.0] |
| 30 | +tspan = (0.0f0, 5.0f0) |
| 31 | +tsteps = range(tspan[1], tspan[2], length = datasize) |
| 32 | + |
| 33 | + |
| 34 | +# Get the data |
| 35 | +function trueODEfunc(du, u, p, t) |
| 36 | + true_A = [-0.1 2.0; -2.0 -0.1] |
| 37 | + du .= ((u.^3)'true_A)' |
| 38 | +end |
| 39 | +prob_trueode = ODEProblem(trueODEfunc, u0, tspan) |
| 40 | +ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps)) |
| 41 | + |
| 42 | + |
| 43 | +# Define the Neural Network |
| 44 | +nn = Lux.Chain(ActivationFunction(x -> x.^3), |
| 45 | + Lux.Dense(2, 16, tanh), |
| 46 | + Lux.Dense(16, 2)) |
| 47 | +p_init, st = Lux.setup(rng, nn) |
| 48 | + |
| 49 | +neuralode = NeuralODE(nn, tspan, Tsit5(), saveat = tsteps) |
| 50 | +prob_node = ODEProblem((u,p,t)->nn(u,p,st)[1], u0, tspan, Lux.ComponentArray(p_init)) |
| 51 | + |
| 52 | + |
| 53 | +function plot_multiple_shoot(plt, preds, group_size) |
| 54 | + step = group_size-1 |
| 55 | + ranges = group_ranges(datasize, group_size) |
| 56 | + |
| 57 | + for (i, rg) in enumerate(ranges) |
| 58 | + plot!(plt, tsteps[rg], preds[i][1,:], markershape=:circle, label="Group $(i)") |
| 59 | + end |
| 60 | +end |
| 61 | + |
| 62 | +# Animate training, cannot make animation on CI server |
| 63 | +# anim = Plots.Animation() |
| 64 | +iter = 0 |
| 65 | +callback = function (p, l, preds; doplot = false) |
| 66 | + display(l) |
| 67 | + global iter |
| 68 | + iter += 1 |
| 69 | + if doplot && iter%1 == 0 |
| 70 | + # plot the original data |
| 71 | + plt = scatter(tsteps, ode_data[1,:], label = "Data") |
| 72 | + |
| 73 | + # plot the different predictions for individual shoot |
| 74 | + plot_multiple_shoot(plt, preds, group_size) |
| 75 | + |
| 76 | + frame(anim) |
| 77 | + display(plot(plt)) |
| 78 | + end |
| 79 | + return false |
| 80 | +end |
| 81 | + |
| 82 | +# Define parameters for Multiple Shooting |
| 83 | +group_size = 3 |
| 84 | +continuity_term = 200 |
| 85 | + |
| 86 | +function loss_function(data, pred) |
| 87 | + return sum(abs2, data - pred) |
| 88 | +end |
| 89 | + |
| 90 | +function loss_multiple_shooting(p) |
| 91 | + return multiple_shoot(p, ode_data, tsteps, prob_node, loss_function, Tsit5(), |
| 92 | + group_size; continuity_term) |
| 93 | +end |
| 94 | + |
| 95 | +adtype = Optimization.AutoZygote() |
| 96 | +optf = Optimization.OptimizationFunction((x,p) -> loss_multiple_shooting(x), adtype) |
| 97 | +optprob = Optimization.OptimizationProblem(optf, Lux.ComponentArray(p_init)) |
| 98 | +res_ms = Optimization.solve(optprob, PolyOpt(), |
| 99 | + callback = callback) |
| 100 | +#gif(anim, "multiple_shooting.gif", fps=15) |
| 101 | +``` |
| 102 | + |
| 103 | +Here's the animation that we get from above when `doplot=true` and the |
| 104 | +animation code is uncommented: |
| 105 | + |
| 106 | + |
| 107 | +The connected lines show the predictions of each group (Notice that there |
| 108 | +are overlapping points as well. These are the points we are trying to coincide.) |
| 109 | + |
| 110 | +Here is an output with `group_size = 30` (which is same as solving on the whole |
| 111 | +interval without splitting also called single shooting) |
| 112 | + |
| 113 | +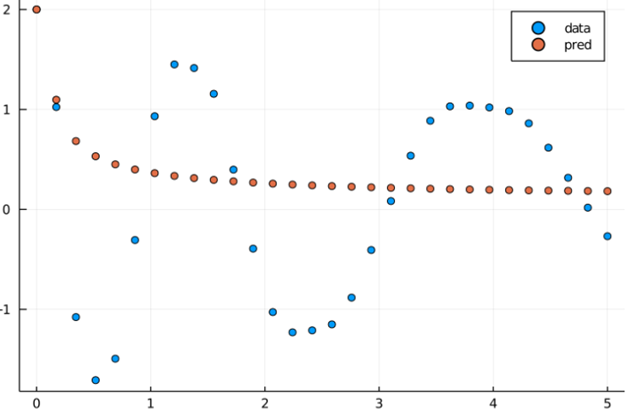 |
| 114 | + |
| 115 | +It is clear from the above picture, a single shoot doesn't perform very well |
| 116 | +with the ODE Problem we have and gets stuck in a local minima. |
0 commit comments