|
1 | 1 | # Comparisons and Set based operations |
2 | 2 |
|
3 | | -Comparisons between p-boxes, intervals, and scalars |
| 3 | +Comparisons |
4 | 4 | --- |
5 | 5 |
|
6 | | - |
| 6 | +Comparisons `(<, >, <=, >=, ==)` between p-boxes, intervals and scalars can be performed. However unlike for comparisons between real numbers which yield Boolean values (`true` or `false`), comparisons with p-boxes generally yield interval probabilities, giving the uncertainty that the random variable characterised by a p-box meets the condition. |
7 | 7 |
|
| 8 | +__*NOTE: unlike `IntervalArithmetic.jl`, comparisons in `ProbabilityBoundsAnalysis.jl` will generally give non-Boolean values (interval probabilities). This may cause crashes when evaluating control-flow (if-else) with uncertainty*__ |
| 9 | + |
| 10 | +### Comparisons of p-boxes and scalars |
| 11 | + |
| 12 | +For a p-box `X` and real number `y`, `X <= y` is the evaluation of y in the CDF of X: |
| 13 | + |
| 14 | +) |
| 15 | + |
| 16 | + |
| 17 | +Similarly, `X >= y` is |
| 18 | + |
| 19 | +) |
| 20 | + |
| 21 | +Example |
| 22 | +```julia |
| 23 | +julia> X = uniform(0, 1) |
| 24 | +julia> X <= 0.7 |
| 25 | +[0.695, 0.705001] |
| 26 | + |
| 27 | +julia> X > 0.4 |
| 28 | +[0.594999, 0.605] |
| 29 | + |
| 30 | +julia> X = normal(interval(-0.5, 0.5), interval(1, 1.5)) |
| 31 | +julia> X >= 1 |
| 32 | +[0.0649999, 0.37] |
| 33 | +``` |
| 34 | + |
| 35 | +Boolean values are returned if condition is gauranteed |
| 36 | + |
| 37 | +```julia |
| 38 | +julia> X = uniform(0, 1) |
| 39 | +julia> X <= 2 |
| 40 | +true |
| 41 | + |
| 42 | +julia> X > 2 |
| 43 | +false |
| 44 | +``` |
| 45 | + |
| 46 | +### Comparisons of p-boxes and intervals |
| 47 | + |
| 48 | +A comparison between a p-box `X` and an interval `Y` can be evaluated as follows |
| 49 | + |
| 50 | + |
| 51 | + |
| 52 | + |
| 53 | +where subtraction is evaluated with p-box arithmetic, and then the resulting p-box's CDF is evaluated at `0`. I.e., `Z = X - Y` and then `cdf(Z, 0.0)`. Similarly |
| 54 | + |
| 55 | +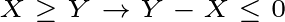 |
| 56 | + |
| 57 | +Example |
| 58 | +```julia |
| 59 | +julia> X = uniform(0, 1) |
| 60 | +julia> Y = interval(0.7, 2) |
| 61 | +julia> X <= Y |
| 62 | +[0.695, 1] |
| 63 | + |
| 64 | +julia> X > Y |
| 65 | +[0, 0.305] |
| 66 | + |
| 67 | +julia> X <= interval(2, 3) |
| 68 | +true |
| 69 | + |
| 70 | +julia> X > interval(2, 3) |
| 71 | +false |
| 72 | +``` |
| 73 | + |
| 74 | +### Comparisons between p-boxes |
| 75 | + |
| 76 | +Comparison between two p-boxes `X` and `Y` are performed similarly to intervals |
| 77 | + |
| 78 | + |
| 79 | + |
| 80 | +However, for arithmetic operation (subtraction) to be performed exactly, the dependence (copula) between `X` and `Y` must be known. The default is _Frechet_ (unknown dependence). Therefore, even if we begin with precise p-boxes (distributions), comparisons will give interval probabilities. |
| 81 | + |
| 82 | +Example |
| 83 | + |
| 84 | +```julia |
| 85 | +julia> X = uniform(0, 1) |
| 86 | +julia> Y = uniform(0.5, 1.5) |
| 87 | +julia> X <= Y |
| 88 | +[0.5, 1] |
| 89 | + |
| 90 | +julia> X <= uniform(2, 3) |
| 91 | +true |
| 92 | + |
| 93 | +julia> X >= uniform(2, 3) |
| 94 | +false |
| 95 | +``` |
| 96 | + |
| 97 | +The correlation (e.g. independence) can be specified when performing the comparison (which uses a gaussian copula as default) |
| 98 | + |
| 99 | + |
| 100 | +```julia |
| 101 | +julia> X = uniform(0, 1) |
| 102 | +julia> Y = uniform(0.5, 1.5) |
| 103 | +julia> <=(X,Y, corr = 0) |
| 104 | +[0.869999, 0.880001] |
| 105 | + |
| 106 | +julia> >(X,Y, corr = 0) |
| 107 | +[0.119999, 0.130001] |
| 108 | + |
| 109 | +julia> <=(X,Y, corr = 1) |
| 110 | +true |
| 111 | + |
| 112 | +julia> <=(X,Y, corr = -1) |
| 113 | +[0.744999, 0.755001] |
| 114 | + |
| 115 | +julia> >(X,Y, corr = 0.5) |
| 116 | +[0.04, 0.0550001] |
| 117 | +``` |
| 118 | + |
| 119 | +Notice that the dependence can greatly change the probability. For example `<=(X,Y, corr = 1)` gave `true` (probability `1`). |
8 | 120 |
|
9 | 121 | Set based operations |
10 | 122 | --- |
@@ -48,13 +160,13 @@ julia> plot(c3, fontsize = 22) |
48 | 160 |  |
49 | 161 |
|
50 | 162 | ### Intersection of p-boxes, intervals, and scalars |
51 | | -If non-empty, set intersection can be performed between p-boxes. The following take the intersection between two normal shaped p-boxes `N([0, 1.5], [1, 2]) ∩ N([1, 2], 1) -> N([1,1.5],1)` |
| 163 | +If non-empty, set intersection can be performed between p-boxes. The following take the intersection between two normal shaped p-boxes `N([0, 1.5], [1, 2]) ∩ N([1, 2], 1) -> N([1, 1.5],1)` |
52 | 164 |
|
53 | 165 | ```julia |
54 | 166 | julia> using ProbabilityBoundsAnalysis, PyPlot, IntervalArithmetic |
55 | 167 | julia> a = normal(0..1.5, 1..2) |
56 | 168 | julia> b = normal(1..2, 1) |
57 | | -julia> c = a ∩ b # or imp(a3, b3) |
| 169 | +julia> c = a ∩ b # or imp(a, b) |
58 | 170 | julia> plot(a, name = "ab", col = "red", fontsize = 22) |
59 | 171 | julia> plot(b, name = "ab", col = "blue", fontsize = 22) |
60 | 172 | julia> plot(c, fontsize = 22) |
|
0 commit comments